Variance in the direction of a vector

Status: half-baked

This all is true in any number of dimensions, but let’s say we measure two things for a bunch of people. Perhaps it is height and weight, who knows. A measurement is then a vector $x = (h, w)$. If we have many measurements we can put them in a matrix $X = (x_1 \ldots x_n)$.

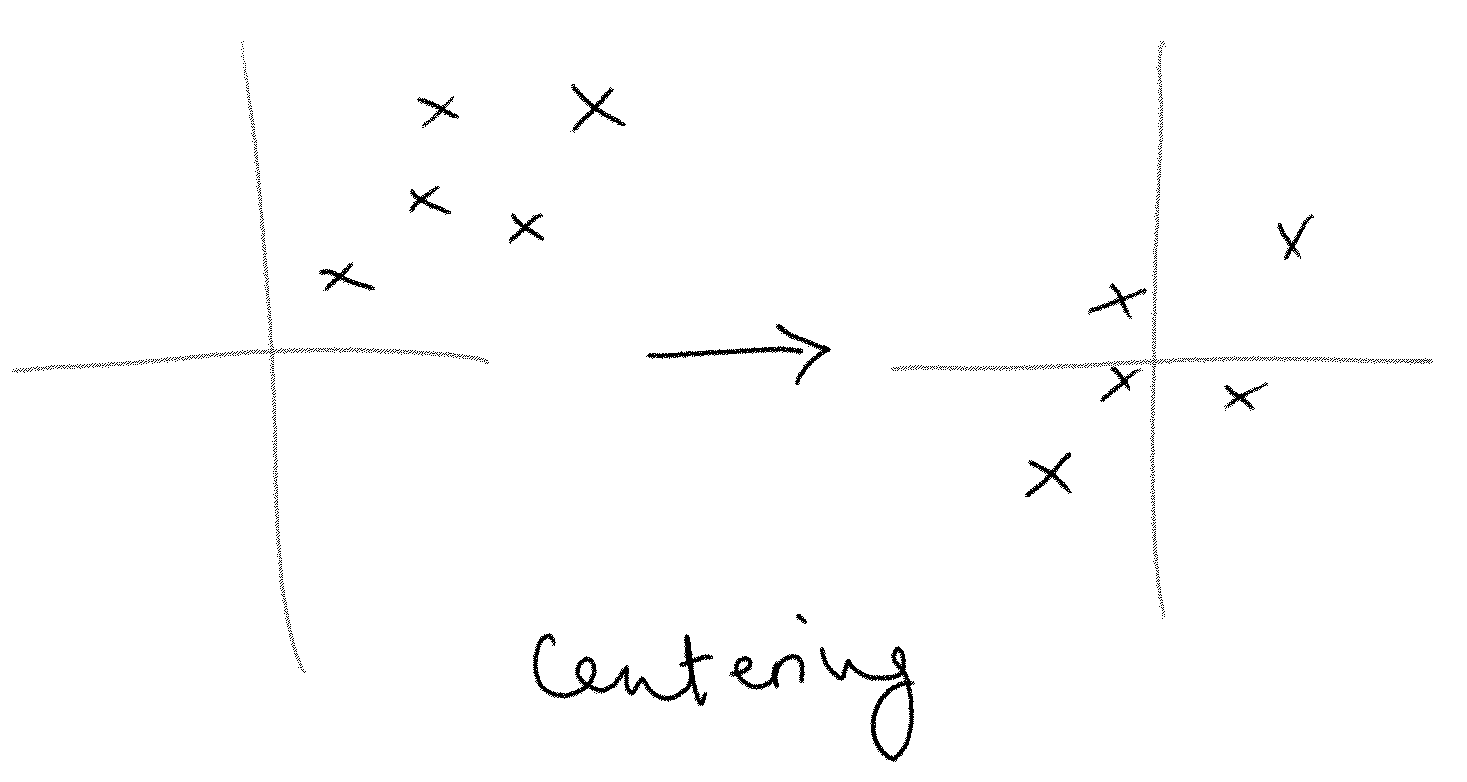
Suppose we center these data by subtracting the average vector from each individual vector so that $\tilde x_i = x_i - m$, with $m = \frac{1}{n} \sum x_i$ being the average. The total variance in these data is $\frac{1}{n} \sum \lVert \tilde x_i\rVert^2$, the average squared length of the centered vectors.

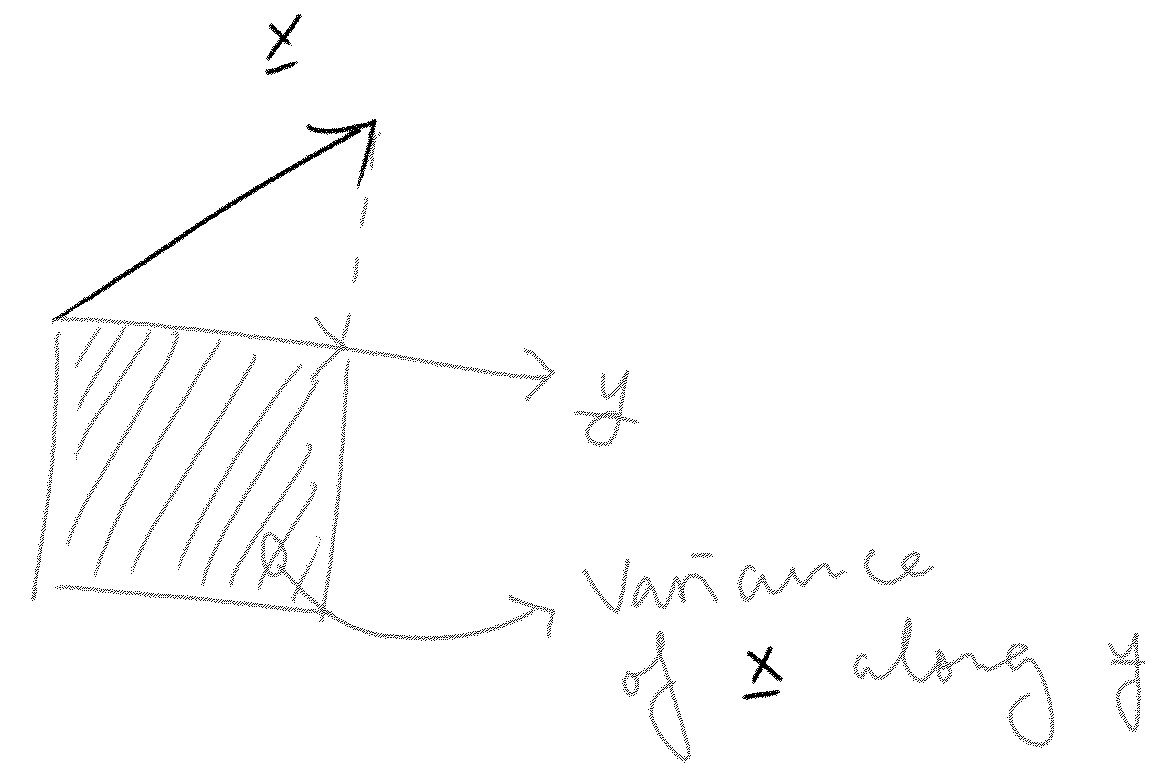
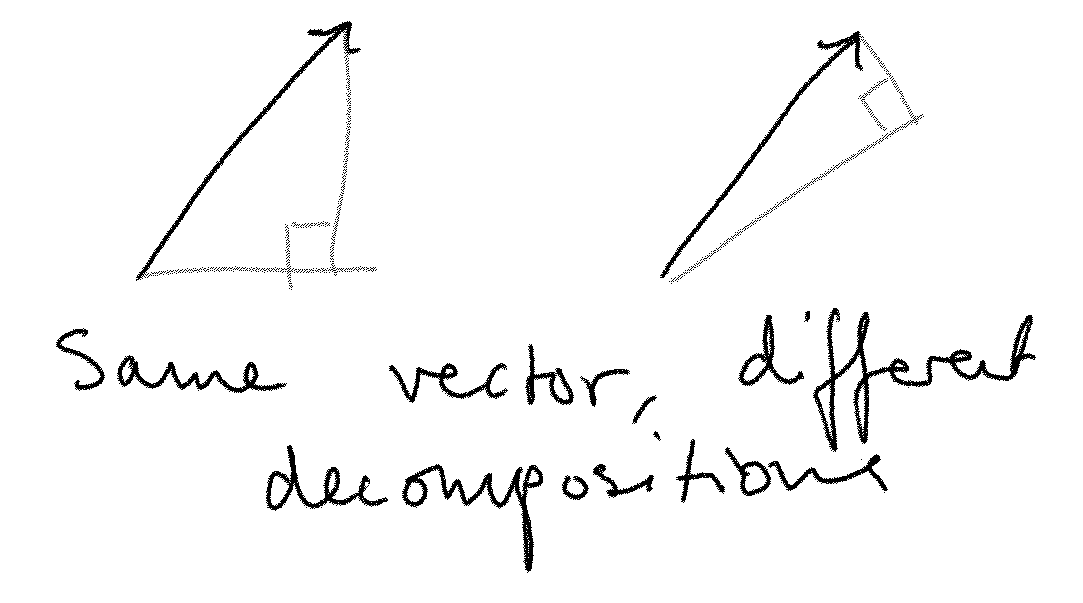
The variance along a particular vector $v$ is just the average squared length of your centered vectors if you project them onto $v$.

For any orthogonal basis $v_1, v_2$ we can have $\tilde x = cv_1 + dv_2$ and because of Pythagoras we will have $\lVert x \rVert^2 = \lVert cv_1 \rVert^2 + \lVert dv_2 \rVert^2$. This means that we can always express the total variance as the sum of variances in orthogonal directions.